Como Funciona a Regressão Logística? Tudo o Que Você Precisa Saber
A regressão logística é uma técnica usada para prever a probabilidade de um evento ocorrer, classificando dados em categorias
Em primeiro lugar, desejo um Feliz 2025 para você! ✨
Que este novo ano seja repleto de conquistas, aprendizados e novas oportunidades. E para começar com o pé direito, vamos explorar um conceito muito interessante: a regressão logística!
A regressão logística é uma técnica amplamente utilizada em análise de dados e aprendizado de máquina, especialmente em tarefas de classificação.
Ao contrário da regressão linear, que é usada para prever variáveis contínuas, a regressão logística é utilizada para prever variáveis categóricas, tipicamente com duas classes (binária) - por exemplo, a probabilidade de um cliente comprar ou não um produto.
Vamos entender como essa técnica funciona e ao final do artigo, colocar a mão na massa com um exemplo prático!
Acesse o Colab (Notebook) com o código: https://elisaterumi.substack.com/p/notebooks
O que é regressão logística?
A regressão logística tem como objetivo modelar a probabilidade de uma variável dependente binária (0 ou 1), com base em uma ou mais variáveis independentes.
A principal ideia por trás do modelo é usar uma função sigmoide (também conhecida como função logística) para transformar a previsão linear em uma probabilidade.
A função sigmoide é uma curva matemática que transforma valores em um intervalo entre 0 e 1, frequentemente usada em modelos de aprendizado de máquina para representar probabilidades.
A equação da regressão logística é expressa como:
Onde:
P(Y=1∣X) é a probabilidade de a variável dependente Y ser igual a 1, dada a variável independente X.
β₀ é o intercepto (ou coeficiente de bias).
β₁ é o coeficiente da variável independente X.
e é a base do logaritmo natural, aproximadamente 2.718.
A função sigmoide mapeia os valores da equação linear para o intervalo de 0 a 1, interpretando esses valores como probabilidades.
Como funciona?
O processo de treinamento de um modelo de regressão logística envolve a estimação dos coeficientes (β₀, β₁, etc.) de modo que o modelo minimize o erro entre as previsões e os valores reais.
A técnica mais comum para otimizar esses coeficientes é o método de máxima verossimilhança, que busca encontrar os valores que tornam os dados mais prováveis, dada a distribuição dos resíduos.
Exemplos de aplicação
Diagnóstico médico: prever se um paciente tem ou não uma doença com base em características como idade, histórico médico e resultados de exames.
Análise de crédito: avaliar se um cliente deve ser aprovado ou não para um crédito, baseado em variáveis como renda, histórico de crédito e outros dados financeiros.
Marketing e vendas: prever a probabilidade de um cliente realizar uma compra com base em seu comportamento de navegação ou em suas características demográficas.
Vantagens da regressão logística
Simples e eficiente: é fácil de entender e interpretar, com uma formulação matemática simples.
Probabilidade como saída: a regressão logística fornece uma saída interpretável como probabilidade, o que é útil em muitas situações de tomada de decisão.
Funciona bem com dados lineares: se a relação entre as variáveis independentes e a variável dependente for linear, a regressão logística será bastante eficaz.
Limitações
Restrita a variáveis binárias: embora existam variações (como a regressão logística multinomial), a regressão logística básica só é adequada para tarefas de classificação binária.
Sensível a outliers: a presença de outliers (valores que fogem do padrão dos dados) pode influenciar de forma significativa a estimação dos coeficientes.
Relações lineares: assume que a relação entre as variáveis independentes e a variável dependente seja linear no logaritmo das probabilidades, o que pode não ser o caso em algumas situações mais complexas.
Diferença entre Regressão Linear e Regressão Logística
A principal diferença entre a regressão linear (que vimos anteriormente) e a regressão logística está no tipo de variável dependente que cada uma trata.
A regressão linear é usada para prever variáveis contínuas, como preço ou temperatura, e modela a relação entre as variáveis independentes e a dependente com uma linha reta.
Já a regressão logística é utilizada quando a variável dependente é binária ou categórica, como "sim" ou "não", e faz previsões de probabilidades, aplicando a função sigmoid para garantir que as saídas estejam entre 0 e 1.
Enquanto a regressão linear gera valores contínuos sem restrições, a regressão logística transforma suas previsões em probabilidades, ideais para classificação.
Mãos à obra!
Vamos continuar com o exemplo que utilizamos no nosso artigo sobre regressão linear, que envolve o número de horas de estudo e a nota dos alunos.
Porém, ao invés de prever diretamente a nota, como fizemos na regressão linear, agora vamos usar a Regressão Logística para prever a probabilidade de um aluno tirar uma nota acima de 8.
Aqui está o código Python para excecutarmos:
import numpy as np
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
# Dados fornecidos no problema
horas_estudo = np.array([2, 3, 4, 5, 6, 7, 8, 9, 10, 11]).reshape(-1, 1)
notas_prova_acima_8 = np.array([0, 0, 0, 1, 1, 1, 1, 1, 1, 1])
# Criar e treinar o modelo de regressão logística
model = LogisticRegression()
model.fit(horas_estudo, notas_prova_acima_8)
# Fazer previsões e calcular a probabilidade para valores no intervalo
x_values = np.linspace(0, 10, 100).reshape(-1, 1)
y_prob = model.predict_proba(x_values)[:, 1]
# Visualizar os resultados
plt.scatter(horas_estudo, notas_prova_acima_8, color="red", label="Dados reais")
plt.plot(x_values, y_prob, color="blue", label="Modelo ajustado")
plt.xlabel("Horas de estudo")
plt.ylabel("Probabilidade de nota acima de 8")
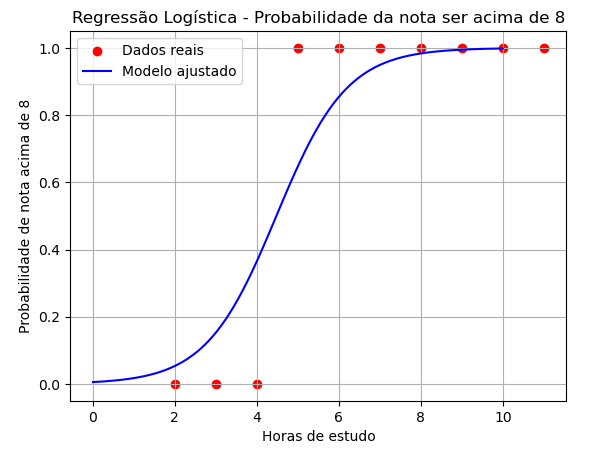
plt.title("Regressão Logística - Probabilidade da nota ser acima de 8")
plt.legend()
plt.grid()
plt.show()
O resultado:
Acesse o Colab (Notebook) com o código: https://elisaterumi.substack.com/p/notebooks
Conclusão
A regressão logística é uma técnica fundamental no campo da estatística e do aprendizado de máquina, sendo amplamente usada em diversas áreas.
Sua capacidade de modelar probabilidades e fornecer resultados interpretáveis a torna uma ferramenta poderosa para resolver problemas de classificação.
Ao entender os conceitos por trás da regressão logística, você estará bem preparado(a) para utilizá-la em uma variedade de cenários de análise de dados.
No próximo post, vamos explorar as árvores de decisão.
Não perca! 💗